|
Явление внутреннего трения с макроскопической точки зрения связано с возникновением сил трения между слоями газа или жидкости, перемещающимися параллельно друг другу с различными по величине скоростями. Со стороны слоя, движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила. Наоборот, медленно перемещающийся слой тормозит более быстро движущиеся слои газа. Силы трения, которые при этом возникают, направлены по касательной к поверхности соприкосновения слоев.
Рассмотрим известный опыт Ньютона. Пусть имеются две параллельные пластинки (рис. 1), между которыми находится газ (жидкость).
 |
| рис. 1 |
Расстояние между пластинками h. Нижнюю пластинку будем удерживать неподвижно, верхнюю заставим двигаться в одном и том же направлении в своей плоскости с постоянной скоростью u0.
Слой газа, непосредственно прилегающий к верхней пластинке, будет иметь ту же скорость u0, что и пластинка, слой же газа, прилегающий к нижней пластинке, находится в покое. Как показывает опыт, любой промежуточный слой движется со скоростью u, пропорциональной расстоянию x от неподвижной пластинки, т. е.
|
 |
(3.3.1) |
Постоянная a определяется из условия, что при x = h u = u0, т. е.
u0 = ah. Откуда a = u0/h. Тогда выражение (3.3.1) примет вид
|
 |
(3.3.2) |
Таким образом, к верхней пластинке приложена сила F1, лежащая в ее плоскости и имеющая то же направление, что и направление движения пластинки. Так как пластинка движется с постоянной скоростью u0, то на пластинку должна действовать такая же по величине, но противоположно направленная сила F со стороны газа, которую назовем силой вязкого трения.
Из опыта следует, что абсолютная величина силы F1 пропорциональна скорости u0, с которой мы двигаем пластинку, и площади пластины, т. е.
|
 |
(3.3.3) |
где  – постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения – постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения  , равенство (3.3.3) перепишем в виде , равенство (3.3.3) перепишем в виде
|
 |
(3.3.4) |
Так как из (3.3.2) следует, что  , то последнее выражение можно представить так: , то последнее выражение можно представить так:
|
 |
(3.3.5) |
Это закон внутреннего вязкого трения Ньютона, который установил его экспериментально. Закон утверждает: при стационарном (ламинарном) движении слоев жидкости или газа с различными скоростями между ними возникают касательные силы, пропорциональные градиенту скорости слоев и площади их соприкосновения. Физический смысл коэффициента вязкости  заключается в том, что он численно равен силе, действующей на единицу площади поверхности, параллельной скорости течения газа или жидкости, при градиенте скорости заключается в том, что он численно равен силе, действующей на единицу площади поверхности, параллельной скорости течения газа или жидкости, при градиенте скорости  . .
Согласно второму закону Ньютона,  , где K – импульс элементарной массы слоя газа. Поэтому (3.3.5) можно представить в виде бесконечно малых: , где K – импульс элементарной массы слоя газа. Поэтому (3.3.5) можно представить в виде бесконечно малых:
|
 |
(3.3.6) |
Пусть изменение скорости движения газа или жидкости происходит в направлении оси X, а сама скорость течения направлена перпендикулярно этой оси (рис. 2).
 |
| рис. 2 |
Тогда закон Ньютона (3.3.6) утверждает: импульс, переносимый за время dt через площадку dS, перпендикулярной оси X, пропорционален времени dt, величине площадки dS и градиенту скорости  . Знак “минус” означает, что импульс переносится в направлении уменьшения скорости слоя. . Знак “минус” означает, что импульс переносится в направлении уменьшения скорости слоя.
С молекулярно-кинетической точки зрения причиной внутреннего трения является наложение упорядоченного движения слоев газа с различными гидродинамическими скоростями u и хаотического теплового движения молекул. В результате теплового движения, молекулы из более быстрого слоя переносят с собой больший упорядоченный импульс  и, сталкиваясь, передают его молекулам более медленно движущегося слоя, вследствие чего он увеличивает скорость. Наоборот, при переходе молекул из медленно движущегося слоя в более быстрый слой, они приносят в него меньший упорядоченный импульс, что приводит к уменьшению упорядоченной скорости этого слоя. Увеличение или уменьшение гидродинамической скорости слоя газа, согласно второму закону динамики, свидетельствует о наличии силы внутреннего трения, действующей между слоями. Следовательно, за счет теплового хаотического движения скорости слоев будут выравниваться, если, конечно, внешними силами не поддерживать разности скоростей слоев. и, сталкиваясь, передают его молекулам более медленно движущегося слоя, вследствие чего он увеличивает скорость. Наоборот, при переходе молекул из медленно движущегося слоя в более быстрый слой, они приносят в него меньший упорядоченный импульс, что приводит к уменьшению упорядоченной скорости этого слоя. Увеличение или уменьшение гидродинамической скорости слоя газа, согласно второму закону динамики, свидетельствует о наличии силы внутреннего трения, действующей между слоями. Следовательно, за счет теплового хаотического движения скорости слоев будут выравниваться, если, конечно, внешними силами не поддерживать разности скоростей слоев.
Таким образом, с точки зрения молекулярно-кинетической теории в процесс внутреннего трения каждая молекула переносит упорядоченный импульс  , вызывая тем самым изменение импульса слоя. Подставляя в общее уравнение переноса (4.4.7) , вызывая тем самым изменение импульса слоя. Подставляя в общее уравнение переноса (4.4.7)  и и 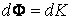 , получим: , получим:
|
 |
(3.3.7) |
Сравнивая последнее соотношение с (3.3.6), получим формулу для коэффициента вязкости газов:
|
 |
(3.3.8) |
Из формулы (3.3.8) видно, что коэффициент вязкости газов, как и коэффициент теплопроводности, не зависит от давления. Опыт подтверждает этот вывод. Отклонения наблюдаются при очень низких и очень высоких давлениях, когда  начинает зависеть от давления. Зависимость начинает зависеть от давления. Зависимость  от температуры такая же, как для коэффициента теплопроводности. от температуры такая же, как для коэффициента теплопроводности.
Наиболее точные методы измерения коэффициента вязкости основаны на формуле Пуазейля:
|
 |
(3.3.9) |
где V – объем газа, протекшего за время t через капилляр радиуса r и длины l при разности давлений  на его концах. Измерив в опыте все указанные величины, из формулы Пуазейля находят коэффициент вязкости на его концах. Измерив в опыте все указанные величины, из формулы Пуазейля находят коэффициент вязкости  . .
|

