|
Адиабатным называют такой процесс, в котором к системе не подво-дится тепло и от системы не отводится тепло. При адиабатном процессе должна быть обеспечена идеальная теплоизоляция от внешней среды, в отличие от изотермического процесса, требующего идеального теплового контакта со средой. В реальных условиях процесс является адиабатным, если система снабжена хорошей теплоизоляцией или если процесс протекает настолько быстро, что не происходит заметного теплообмена с внешней средой.
Из первого закона термодинамики следует, что при адиабатном процессе 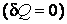 работа производится только за счет изменения внутренней энергии вещества: работа производится только за счет изменения внутренней энергии вещества:
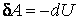 |
(4.9.1) |
Можно записать и в интегральной форме:
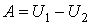 |
(4.9.2) |
Если вещество расширяется и совершает работу над внешними телами, то 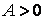 и, как следует , и, как следует , 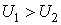 , т. е. внутренняя энергия вещества уменьшается. Это и понятно: в адиабатном процессе к системе нет притока теплоты извне и единственный источник энергии для совершения работы – это внутренняя энергия самой системы. Соотношения справедливы для любых адиабатных процессов: равновесных или неравновесных, для любых веществ, находящихся в любых агрегатных состояниях, так как они являются следствием закона сохранения энергии. , т. е. внутренняя энергия вещества уменьшается. Это и понятно: в адиабатном процессе к системе нет притока теплоты извне и единственный источник энергии для совершения работы – это внутренняя энергия самой системы. Соотношения справедливы для любых адиабатных процессов: равновесных или неравновесных, для любых веществ, находящихся в любых агрегатных состояниях, так как они являются следствием закона сохранения энергии.
Для идеального газа:
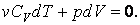 |
(4.9.3) |
Отсюда видно, что при адиабатном расширении 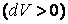 газ охлаждается газ охлаждается 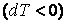 , а при адиабатном сжатии , а при адиабатном сжатии 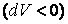 газ нагревается газ нагревается 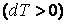 , хотя теплота при этом процессе не подводится и не отводится. , хотя теплота при этом процессе не подводится и не отводится.
Проинтегрировав, найдем работу, совершаемую идеальным газом при адиабатном процессе.
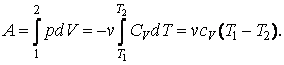 |
(4.9.4) |
Теплоемкость 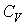 вынесена из-под интеграла, т. к. для идеального газа она не зависит от температуры. вынесена из-под интеграла, т. к. для идеального газа она не зависит от температуры.
Чтобы найти уравнение адиабаты в переменных 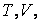 подставим вместо p его выражение из уравнения Менделеева –Клапейрона подставим вместо p его выражение из уравнения Менделеева –Клапейрона 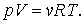 В результате будем иметь В результате будем иметь
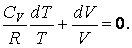 |
(4.9.5) |
Интегрирование последнего соотношения дает
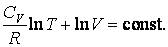 |
(4.9.6) |
Откуда находим
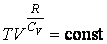 |
(4.9.7) |
Выразим величину 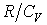 через отношение теплоемкостей через отношение теплоемкостей 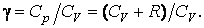 В результате будем иметь В результате будем иметь 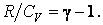 Подставив, получим Подставив, получим
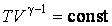 |
(4.9.8) |
Последнее соотношение есть уравнение адиабаты (уравнение Пуассона) в переменных T,V. Чтобы записать это уравнение в координатах p,V или T,p нужно произвести замену соответствующих переменных , воспользовавшись уравнением Менделеева – Клапейрона. В результате получим еще два эквивалентных уравнения адиабаты:
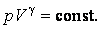 |
(4.9.9) |
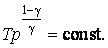 |
(4.9.10) |
Выражение для работы можно записать иначе. Для этого уравнение адиабаты представим в виде:
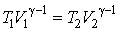 |
(4.9.11) |
Отсюда находим
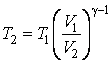 |
(4.9.12) |
Подставляя, и учитывая что 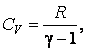 получим
получим
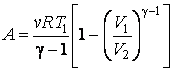 |
(4.9.13) |
Из уравнения Пуассона (4.9.9) следует, что давление идеального газа в адиабатном процессе 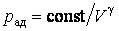 убывает быстрее, чем в изотермическом процессе убывает быстрее, чем в изотермическом процессе 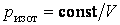 , так как всегда , так как всегда 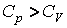 и, таким образом, и, таким образом,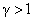 . Физически это объясняется тем, что при адиабатном расширении давление газа уменьшается не только за счет уменьшения объема, но и по причине происходящего при этом понижении температуры. Поэтому и работа против меньшего внешнего давления . Физически это объясняется тем, что при адиабатном расширении давление газа уменьшается не только за счет уменьшения объема, но и по причине происходящего при этом понижении температуры. Поэтому и работа против меньшего внешнего давления 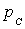 ( ( 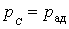 для равновесного процесса) при адиабатном процессе будет меньше, чем работа против большего внешнего давления для равновесного процесса) при адиабатном процессе будет меньше, чем работа против большего внешнего давления 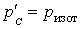 при изотермическом процессе. На рис. 1 работа расширения от объема при изотермическом процессе. На рис. 1 работа расширения от объема 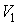 до объема до объема 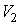 при адиабатном процессе равна площади фигуры при адиабатном процессе равна площади фигуры 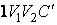 , а при изотермическом – площади фигуры , а при изотермическом – площади фигуры 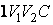 . .
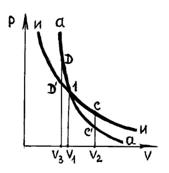 |
| рис. 1 |
Наоборот, при адиабатном сжатии от объема 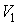 до объема до объема 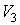 давление газа растет быстрее, чем при изотермическом процессе, так как при адиабатном процессе давление увеличивается не только за счет уменьшения объема, но и вследствие роста температуры газа. Поэтому и работа при адиабатическом сжатии, равная площади фигуры давление газа растет быстрее, чем при изотермическом процессе, так как при адиабатном процессе давление увеличивается не только за счет уменьшения объема, но и вследствие роста температуры газа. Поэтому и работа при адиабатическом сжатии, равная площади фигуры 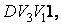 больше работы сжатия при изотермическом процессе, равной площади фигуры больше работы сжатия при изотермическом процессе, равной площади фигуры 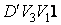 . .
| 
