МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Формуладля КПД цикла Карно получена в предположении, что рабочим веществом являлся идеальный газ. Однако эта формула верна для любых рабочих веществ, используемых в цикле Карно, что доказывает следующая теорема.

Первая теорема Карно. КПД обратимого цикла Карно, осуществляемого между двумя источниками теплоты, не зависит от свойств рабочего вещества, с помощью которого этот цикл осуществляется.

Рассмотрим два тепловых двигателя, работающих между одними и теми же горячим и холодным источниками, но с разными рабочими веществами. Оба двигателя работают по обратимым циклам Карно. Пусть каждый из тепловых двигателей отбирает от горячего источника за цикл одно и тоже количество тепла, равное . Этого всегда можно добиться, т. к. КПД теплового двигателя не зависит от количества рабочего вещества. Если задано количество рабочего вещества, участвующего в цикле в одном из двигателей, то всегда можно подобрать количество рабочего вещества в другом двигателе таким, чтобы количество теплоты, отбираемое первым и вторым двигателями было одинаковым, т. е. . Тогда КПД этих двигателей будут равны:

(4.12.1)

(4.12.2)

рис. 1

Тогда работа, производимая первым двигателем, согласно формуле

(4.12.3)

а работа, потребляемая от первого двигателя вторым,

(4.12.4)

Просуммируем левые и правые части равенств (4.12.3–4.12.4). В результате будем иметь:

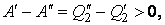(4.12.5)

Таким образом, в результате совместной работы двух двигателей состояние горячего источника не изменилось (первый двигатель за цикл отнял у него количество тепла , второй двигатель за цикл вернул такое же количество тепла), холодный же источник отдал за цикл количество тепла и за счет этого тепла, согласно формуле (4.12.5), совершена положительная работа.

Этот вывод противоречит второму закону термодинамики в формулировке Кельвина. Поэтому предположение, что неверно.

Остается предположить, что . В этом случае, включив второй двигатель в прямом, а первый – в обратном направлении, и, проведя аналогичные рассуждения, придем к выводу, что возможен вечный двигатель второго рода. Следовательно, и это предположение неверно. Остается единственный вариант Таким образом, теорема Карно доказана.

Вторая теорема Карно. КПД необратимого цикла Карно всегда меньше обратимого цикла Карно, осуществляемого между одними и теми же источниками теплоты, имеющими постоянные, но разные температуры.

(4.12.6)

Рассмотрим прямой обратимый цикл Карно. Как мы знаем, чтобы в прямом цикле рабочее вещество обратимо получало тепло и расширялось по изотерме 12, его температура должна быть на бесконечно малую величину меньше температуры горячего источника , т. е.

(4.12.7)

Чтобы рабочее вещество обратимо отдавало тепло при сжатии (на изотерме 34), его температура должна быть на бесконечно малую величину больше температуры холодного источника , т. е.

(4.12.8)

Подставляя выражения (4.12.7–4.12.8) в (4.12.6) и пренебрегая бесконеч-но малыми, получим КПД обратимого цикла Карно равен

(4.12.9)

Для необратимого прямого цикла Карно разности между температурами источников теплоты и рабочего вещества имеют конечное значение:

(4.12.10)

(4.12.11)

что КПД необратимого цикла Карно

(4.12.12)

Сравнивая соотношения (4.12.9) и (4.12.12), заключаем, что

(4.12.13)

Неравенство (4.12.13) получено с учетом одной только внешней необратимости цикла Карно – конечной разности температур между рабочим веществом и источником теплоты. В реальных циклах имеются и внутренние необратимости циклов: процесс трения (при этом часть полезной работы за цикл тратится на трение, что уменьшает КПД цикла), отсутствие механического равновесия (в этом случае давление газа на конечную величину больше или меньше внешнего давления среды) и другие. Все эти необратимости в цикле Карно приводят к уменьшению полезной работы, а, значит, к еще большему усилению неравенства (4.12.13). Следовательно, и вторая теорема Карно доказана.

Третья теорема Карно. Обратимый цикл Карно имеет наибольший КПД по сравнению с любыми обратимыми или необратимыми циклами, в которых наибольшая и наименьшая температуры равны соответственно температуре горячего источника и температуре холодного источника цикла Карно.

Рассмотрим произвольный обратимый цикл, в котором температура рабочего вещества изменяется произвольным образом. В этом случае его невозможно провести обратимо, располагая только двумя источниками тепла с постоянными температурами. Если в начальном состоянии температура рабочего вещества и будет отличаться от температуры источника на бесконечно малую величину, то при дальнейшем изменении температуры рабочего вещества она может оказаться больше (или меньше) температуры источника тепла на конечную величину, что приведет к необратимому процессу теплопроводности и сам процесс станет необратимым. Поэтому для того, чтобы произвольный цикл был обратим, необходимо располагать бесконечно большим числом источников тепла, температуры которых отличаются на бесконечно малую величину.

Введение в теоретическую схему множества источников тепла производится для произвольного цикла следующим образом (рис. 2):

рис. 2

Проведем через этот обратимый цикл адиабаты, бесконечно близко расположенные друг к другу. При этом линии и процесса разобьются на бесконечно малые отрезки, через середины которых проведем изотермы, которые соединят ближайшие адиабаты. В результате таких манипуляций весь цикл разобьется бесконечно узкими циклами Карно. На каждом -м цикле рабочее вещество получает количество тепла от -го горячего источника, находящегося при температуре и отдает количество тепла i-му холодному источнику, имеющему температуру T_2i . Совокупность элементарных циклов Карно вполне эквивалентна первоначальному произвольному циклу. В самом деле, поскольку каждая из адиабат, исключая две крайние, проходится в совокупности дважды и при этом в разных направлениях, суммарная работа цикла при замене его элементарными циклами Карно остается неизменной. Количество же тепла Q1, получаемое процессом на линии 1a2, равно суммарному количеству тепла, получаемому в элементарных изотермах цикла Карно на томже пути 1a2, т. е.

(4.12.14)

а отдаваемая теплота на линии 2b1 будет равна:

(4.12.15)

Таким образом, при бесконечно большом числе источников тепла, с которыми рабочее вещество обменивается теплом, произвольный цикл становится обратимым. При этом его КПД

(4.12.16)

КПД элементарного i -го цикла Карно можно записать в виде:

(4.12.17)

Откуда находим

(4.12.18)

После небольших выкладок имеем Подставляя в формулу (4.12.16) вместо Q₂ меньшую величину , получим

(4.12.19)

Таким образом, КПД произвольного обратимого цикла не может быть больше КПД обратимого цикла Карно, протекающего между наибольшей температурой T₁ и наименьшей температурой T₂ этого произвольного цикла.

Фундаментальное значение доказанной теоремы состоит в том, что она устанавливает наибольший предел КПД тепловых двигателей, к которому должен стремиться инженер-теплотехник в своей исследовательской работе.